Transportstrecke/en: Unterschied zwischen den Versionen
Ferrao (Diskussion | Beiträge) (Die Seite wurde neu angelegt: „A wave runoff calculation is performed for pipes according to Kalinin-Miljukov. The parameters of the Kalinin-Miljukov method are estimated internally by the p…“) |
Keine Bearbeitungszusammenfassung |
||
| (34 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<languages/> | <languages/> | ||
{{Navigation|vorher= | {{Navigation|vorher=Einleitung|hoch=Beschreibung der Systemelemente|nachher=Verbraucher}} | ||
__TOC__ | __TOC__ | ||
[[ | [[Datei:Systemelement003.png|50px|none]] | ||
Transport reaches | Transport reaches simulate the translation and retention behavior of natural water courses or pipelines. There are different approaches for the calculation of pipes or natural channels. | ||
The following options are implemented: | The following options are implemented: | ||
[[ | [[Datei:Berechnungsoptionen_Transportstrecke_EN.png|frame|none|Calculation options for transport reaches]] | ||
==Translation== | ==Translation== | ||
The inflow wave is | The inflow wave is output at the outlet with a time offset that corresponds to the flow time in the transport reach. If the flow time is smaller than the simulation time step, the translation behavior is not visible in the simulation results. | ||
== | <span id="Freispiegel-Rohrleitung"></span> | ||
==Non-Pressurized Pipeline== | |||
This option encompasses flow routing calculation for pipes according to Kalinin-Miljukov. The parameters required by the Kalinin-Miljukov method are estimated internally according to /Euler, 1983/ for circular pipes, and for non-circular profiles, are determined from the hydraulic diameter and the cross-sectional area when completely filled. | |||
{| | {| | ||
| | |Characteristic length: ||<math>L=0.4 \cdot \frac{D}{I_S}~\mbox{[m]} </math> | ||
|- | |- | ||
| | |Retention constant: ||<math>0.64 \cdot L \cdot \frac{D^2}{Q_v} ~\mbox{[s]}</math> | ||
|- | |- | ||
|} | |} | ||
| Zeile 30: | Zeile 31: | ||
|<math>D~\mbox{[m]}</math>: || Circular pipe diameter or hydraulic diameter | |<math>D~\mbox{[m]}</math>: || Circular pipe diameter or hydraulic diameter | ||
|- | |- | ||
|<math>I_S~\mbox{[-]}</math>: || | |<math>I_S~\mbox{[-]}</math>: || Slope of the pipe | ||
|- | |- | ||
|<math>Q_v ~\mbox{[m³/s]}</math>: || | |<math>Q_v ~\mbox{[m³/s]}</math>: || Discharge capacity of the pipe when completely filled | ||
|- | |- | ||
|} | |} | ||
The | The discharge capacity of the pipe when completely filled is calculated according to the flow law of Prandtl-Colebrook: | ||
<math>Q_v=A_v \left [ -2 \cdot \lg \left [\frac{251 \cdot \nu}{D \sqrt{2 g D I_S}} + \frac{k_b}{3.71 \cdot D} \right ] \cdot \sqrt{2gDI_s} \right ]</math> | <math>Q_v=A_v \left [ -2 \cdot \lg \left [\frac{251 \cdot \nu}{D \sqrt{2 g D I_S}} + \frac{k_b}{3.71 \cdot D} \right ] \cdot \sqrt{2gDI_s} \right ]</math> | ||
| Zeile 42: | Zeile 43: | ||
with: | with: | ||
{|style="margin-left: 40px;" | {|style="margin-left: 40px;" | ||
|<math>A_v~\mbox{[m²]}</math>: || | |<math>A_v~\mbox{[m²]}</math>: || Cross-sectional area of the profile | ||
|- | |- | ||
|<math>\nu~\mbox{[m²/s]}</math>: || | |<math>\nu~\mbox{[m²/s]}</math>: || Kinematic viscosity | ||
|- | |- | ||
|<math>k_b ~\mbox{[ | |<math>k_b ~\mbox{[m]}</math>: || Operating roughness | ||
|- | |- | ||
|<math>g ~\mbox{[m/s²]}</math>: || Gravitational | |<math>g ~\mbox{[m/s²]}</math>: || Gravitational acceleration | ||
|- | |- | ||
|} | |} | ||
Using the characteristic length <math>L</math>, the length of the transport reach <math>L_g</math> is divided into <math>n</math> calculation sections of equal length with | |||
::<math>n=L_g/L</math> ( | ::<math>n=L_g/L</math> (where <math>n</math> is an integer number) | ||
Parameters are adjusted as follows for the individual calculation sections: | |||
::<math>L^*=L_g/n</math> | ::<math>L^*=L_g/n</math> | ||
::<math>K^*=K \cdot L^*/L</math> | ::<math>K^*=K \cdot L^*/L</math> | ||
Based on these parameters, after calculating the following recursion formula <math>n</math> times, | |||
<math>Q_{a,i}=Q_{a,i-1}+C_1 \cdot \left(Q_{z,i-1} - Q_{a,i-1} \right ) + C_2 \cdot \left(Q_{z,i}-Q_{z,i-1} \right) </math> | <math>Q_{a,i}=Q_{a,i-1}+C_1 \cdot \left(Q_{z,i-1} - Q_{a,i-1} \right ) + C_2 \cdot \left(Q_{z,i}-Q_{z,i-1} \right) </math> | ||
with: | |||
{|style="margin-left: 40px;" | {|style="margin-left: 40px;" | ||
|<math>Q_z</math>: || | |<math>Q_z</math>: || Inflow to calculation section | ||
|- | |- | ||
|<math>Q_a</math>: || | |<math>Q_a</math>: || Outflow from calculation section | ||
|- | |- | ||
|<math>i</math>: || | |<math>i</math>: || Current calculation time step | ||
|- | |- | ||
|<math>i-1</math>: || | |<math>i-1</math>: || Previous calculation time step | ||
|- | |- | ||
|<math>dt</math>: || | |<math>dt</math>: || Calculation time interval | ||
|- | |- | ||
|<math>C_1=1- e^{-dt/K^*}</math> || | |<math>C_1=1- e^{-dt/K^*}</math> || | ||
| Zeile 82: | Zeile 83: | ||
|- | |- | ||
|} | |} | ||
produces the outflow at the end of the pipe. | |||
This approximation method derived from Kalinin-Miljukov is identical to the linear storage cascade used for calculating runoff concentration. This means the flow ina transport reach can be simulated using a linear storage cascade consisting of <math>n</math> storages with the retention constant <math>K^*</math>. | |||
<span id="Offenes_Gerinne_mit_Angabe_eines_Querprofiles"></span> | |||
==Cross-Section (Open Channel)== | |||
As with non-pressurized pipelines, the translation and retention behavior is simulated using flow routing according to Kalinin-Miljukov. The characteristic length required as a parameter for the Kalinin-Miljukov method is derived from the steady uniform flow relationship according to Manning-Strickler /Rosemann, 1970/. | |||
[[Datei:Schema_charakteristische_Länge_EN.png|400px]] | |||
The channel is divided into individual segments with the characteristic length. For each segment, the calculation of flow routing is carried out using [[Special:MyLanguage/Berechnungsschema von Speichern|nonlinear storage calculation]] with the help of the steady uniform flow relation. | |||
== | <span id="Kennlinie_(Wasserspiegel_–_Querschnittsfläche_–_Abfluss)"></span> | ||
==Rating Curve (Open Channel)== | |||
If the flow behavior of the transport reach is known, e.g. from previous hydraulic calculations, a rating curve defining the relationship between water level, cross sectional area and discharge can be used. | |||
Aktuelle Version vom 15. Januar 2025, 12:15 Uhr
Transport reaches simulate the translation and retention behavior of natural water courses or pipelines. There are different approaches for the calculation of pipes or natural channels.
The following options are implemented:
Translation
The inflow wave is output at the outlet with a time offset that corresponds to the flow time in the transport reach. If the flow time is smaller than the simulation time step, the translation behavior is not visible in the simulation results.
Non-Pressurized Pipeline
This option encompasses flow routing calculation for pipes according to Kalinin-Miljukov. The parameters required by the Kalinin-Miljukov method are estimated internally according to /Euler, 1983/ for circular pipes, and for non-circular profiles, are determined from the hydraulic diameter and the cross-sectional area when completely filled.
| Characteristic length: | [math]\displaystyle{ L=0.4 \cdot \frac{D}{I_S}~\mbox{[m]} }[/math] |
| Retention constant: | [math]\displaystyle{ 0.64 \cdot L \cdot \frac{D^2}{Q_v} ~\mbox{[s]} }[/math] |
with:
| [math]\displaystyle{ D~\mbox{[m]} }[/math]: | Circular pipe diameter or hydraulic diameter |
| [math]\displaystyle{ I_S~\mbox{[-]} }[/math]: | Slope of the pipe |
| [math]\displaystyle{ Q_v ~\mbox{[m³/s]} }[/math]: | Discharge capacity of the pipe when completely filled |
The discharge capacity of the pipe when completely filled is calculated according to the flow law of Prandtl-Colebrook:
[math]\displaystyle{ Q_v=A_v \left [ -2 \cdot \lg \left [\frac{251 \cdot \nu}{D \sqrt{2 g D I_S}} + \frac{k_b}{3.71 \cdot D} \right ] \cdot \sqrt{2gDI_s} \right ] }[/math]
with:
| [math]\displaystyle{ A_v~\mbox{[m²]} }[/math]: | Cross-sectional area of the profile |
| [math]\displaystyle{ \nu~\mbox{[m²/s]} }[/math]: | Kinematic viscosity |
| [math]\displaystyle{ k_b ~\mbox{[m]} }[/math]: | Operating roughness |
| [math]\displaystyle{ g ~\mbox{[m/s²]} }[/math]: | Gravitational acceleration |
Using the characteristic length [math]\displaystyle{ L }[/math], the length of the transport reach [math]\displaystyle{ L_g }[/math] is divided into [math]\displaystyle{ n }[/math] calculation sections of equal length with
- [math]\displaystyle{ n=L_g/L }[/math] (where [math]\displaystyle{ n }[/math] is an integer number)
Parameters are adjusted as follows for the individual calculation sections:
- [math]\displaystyle{ L^*=L_g/n }[/math]
- [math]\displaystyle{ K^*=K \cdot L^*/L }[/math]
Based on these parameters, after calculating the following recursion formula [math]\displaystyle{ n }[/math] times,
[math]\displaystyle{ Q_{a,i}=Q_{a,i-1}+C_1 \cdot \left(Q_{z,i-1} - Q_{a,i-1} \right ) + C_2 \cdot \left(Q_{z,i}-Q_{z,i-1} \right) }[/math]
with:
| [math]\displaystyle{ Q_z }[/math]: | Inflow to calculation section |
| [math]\displaystyle{ Q_a }[/math]: | Outflow from calculation section |
| [math]\displaystyle{ i }[/math]: | Current calculation time step |
| [math]\displaystyle{ i-1 }[/math]: | Previous calculation time step |
| [math]\displaystyle{ dt }[/math]: | Calculation time interval |
| [math]\displaystyle{ C_1=1- e^{-dt/K^*} }[/math] | |
| [math]\displaystyle{ C_2=1- \frac{K^*}{dt}/C_1 }[/math] |
produces the outflow at the end of the pipe. This approximation method derived from Kalinin-Miljukov is identical to the linear storage cascade used for calculating runoff concentration. This means the flow ina transport reach can be simulated using a linear storage cascade consisting of [math]\displaystyle{ n }[/math] storages with the retention constant [math]\displaystyle{ K^* }[/math].
Cross-Section (Open Channel)
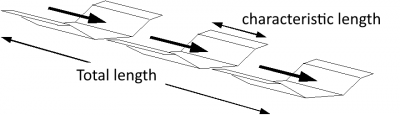
As with non-pressurized pipelines, the translation and retention behavior is simulated using flow routing according to Kalinin-Miljukov. The characteristic length required as a parameter for the Kalinin-Miljukov method is derived from the steady uniform flow relationship according to Manning-Strickler /Rosemann, 1970/.
The channel is divided into individual segments with the characteristic length. For each segment, the calculation of flow routing is carried out using nonlinear storage calculation with the help of the steady uniform flow relation.
Rating Curve (Open Channel)
If the flow behavior of the transport reach is known, e.g. from previous hydraulic calculations, a rating curve defining the relationship between water level, cross sectional area and discharge can be used.